AI Approaches
In our study, we used two different approaches to meet the goals highlighted in the introduction., The first approach focuses on methods to show the potential to reduce preheating and drying times using endpoint prediction, and the second approach focuses on using a digital twin to simulate the process with modified configurations in order to find the best setup.
Endpoint Prediction Study
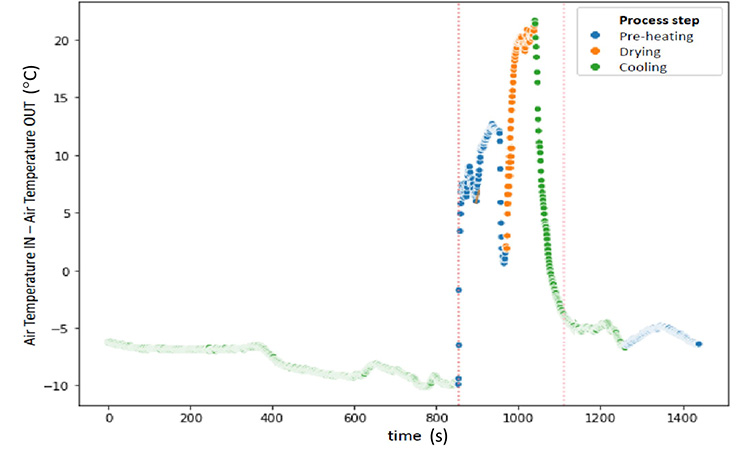
During this process step, the wet granule is not uploaded yet. The supplied energy is used to heat the empty equipment. Once the stainless steel reaches the targeted temperature, the equipment remains at a stable temperature awaiting the next step (drying of loaded product). Any extension of this time causes energy consumption without positive contribution to quality or process duration.
The model used to identify the step endpoint is based on forecasting the step duration by predicting the minimum difference between IN and OUT temperatures when the equipment reaches stability. Thus, the optimal endpoint for the preheating phase is calculated as the forecasted function derivative=0 and the linked time is given as the outcome of the algorithm.
Preheating modeling results
Due to the proportion between rows and columns in the training data, dimensionality reduction techniques are used to minimize the number of features. Data normalization and principal components analysis (PCA). were used, with the model being based on PCA and multiple linear regression.
The metric for evaluating the models is R2 (determination coefficient), which conveys the percentage of the variance explained by the model. The trained model reached R2=0.88 and showed appropriate predictions with equal R2 on the 25% of data reserved for validation purposes.
Time reduction targeted a significant reduction of 37 minutes per batch, leading to an increased equipment availability of 24% and energy savings of 4000 KWh per year (90 batches/year with an average reduction of 45 kWh/batch from the preheating step).
Drying modeling results
The same process was applied to the preheating phase. The combined results are summarized in Table 1.
Table 1: Results of preheating and drying modeling.
| Process step |
R2 |
Time reduction |
Energy savings |
| Preheating |
0.88 |
37 min/batch |
4000 kWh/year |
| Drying |
0.85 |
14 min/batch |
1500 kWh/yea |
| Total sum |
|
51 min/batch |
5500 kWh/year |
In addition to these savings, there are process gains in duration stability and a significant reduction in variability of the results when comparing the production before and after the AI algorithm implementation.
Digital Twin Study
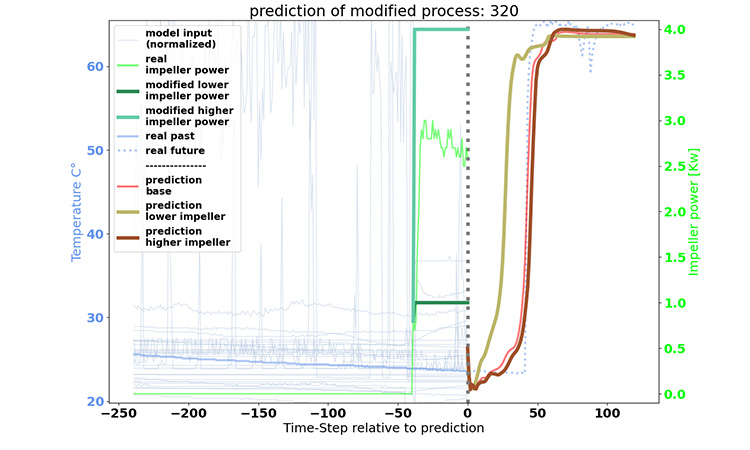
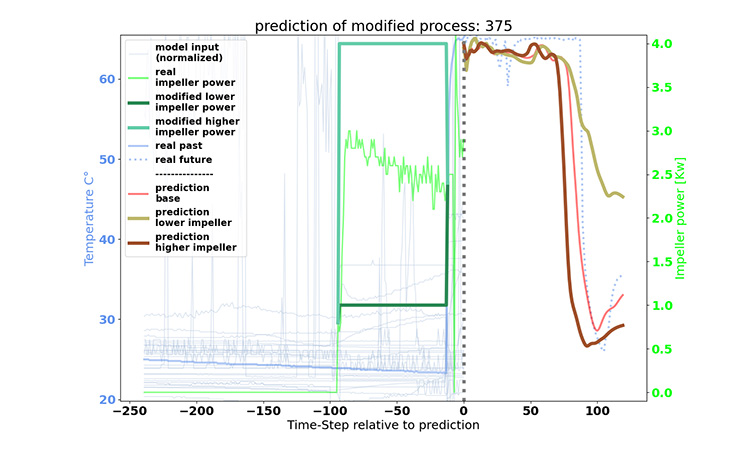
In our second approach, we enabled simulations of the drying process digitally on the computer. A neural network was trained and fed with input parameters measured with the sensors of the fluid bed dryer to predict the evolution of the drying process. In this exercise, we use the neural network model built to predict the behavior using new values on input parameters. This will enable us to conduct cheap and easy testing with the computer instead of producing costly experiments in real life.
In other words, we generated a virtual representation of the drying process for studies in the digital world, which can provide feedback to the real drying process. Such concepts have become known as “digital twins” in recent years,, a term we want to adopt here.
For the digital twin, we need an algorithm capable of processing time-series data, i.e., a multitude of time-series data points as input data, and a few time-series data points as output data. One of the few algorithms that can do this are recurrent neural networks, or, more specifically, long-short term memory neural networks (LSTM).
An LSTM is generated by predefining an architecture of functions that process a certain input in order to relate it to a certain output. Each of the functions contain weights that, in an iterative process, are configured in a way to optimally transfer the input to its associated output. By doing so, we imply that the model learns all the relations and interactions between the set of input parameters and their response and is capable of representing them in a formal mathematical way. This learning process is called model training and is done on large amounts of historical data.
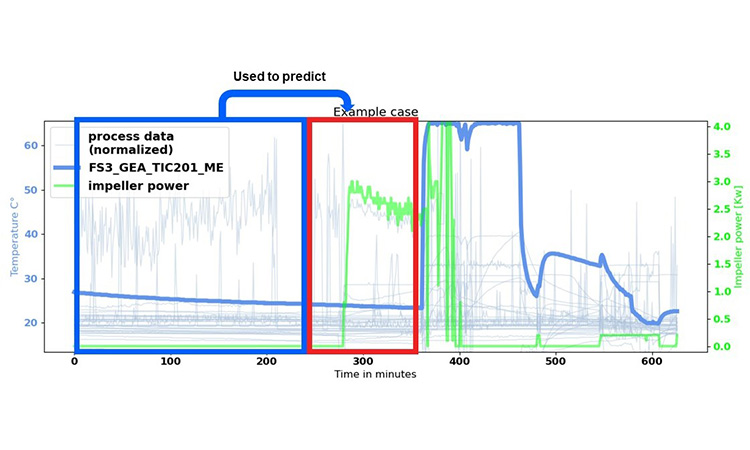
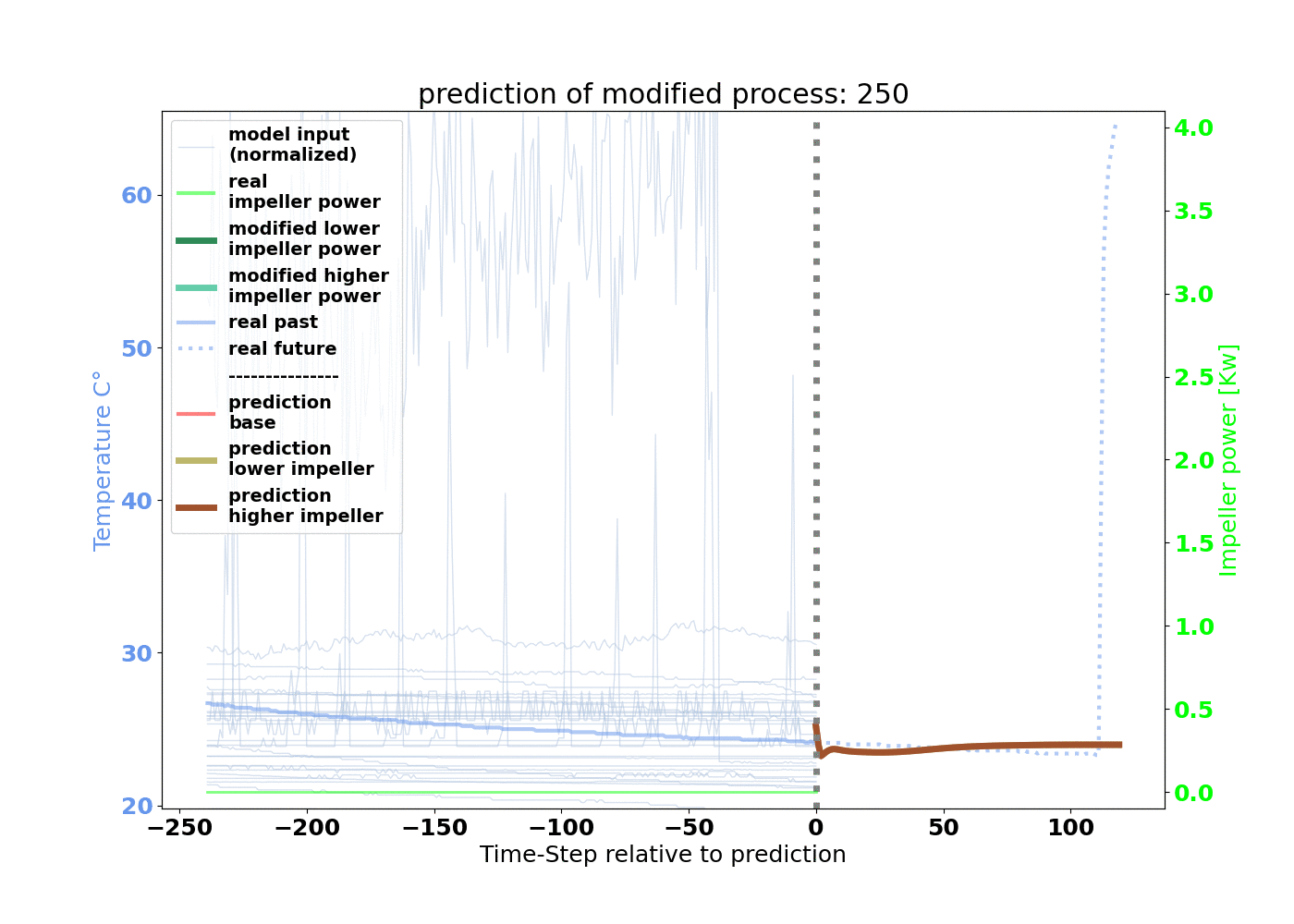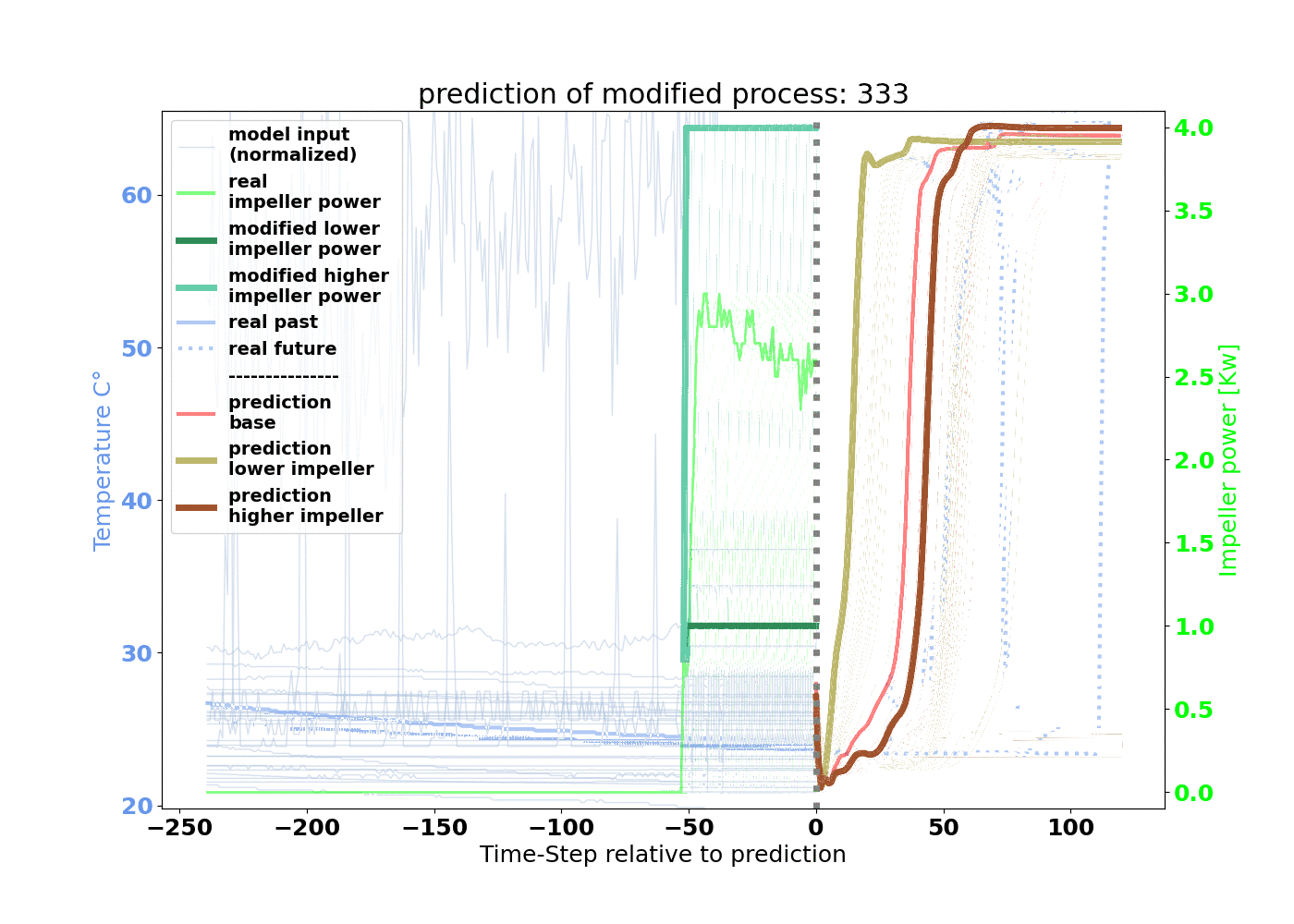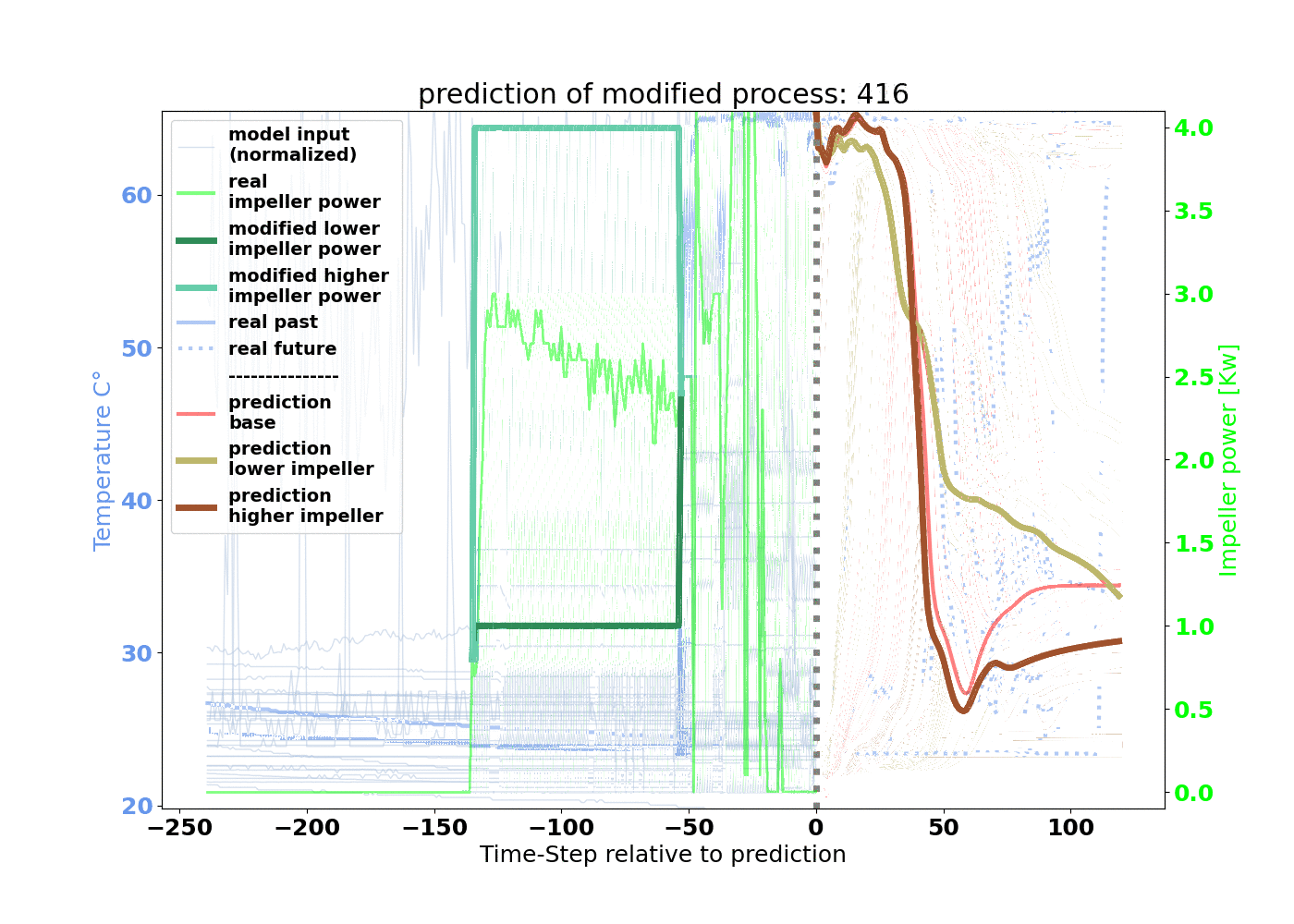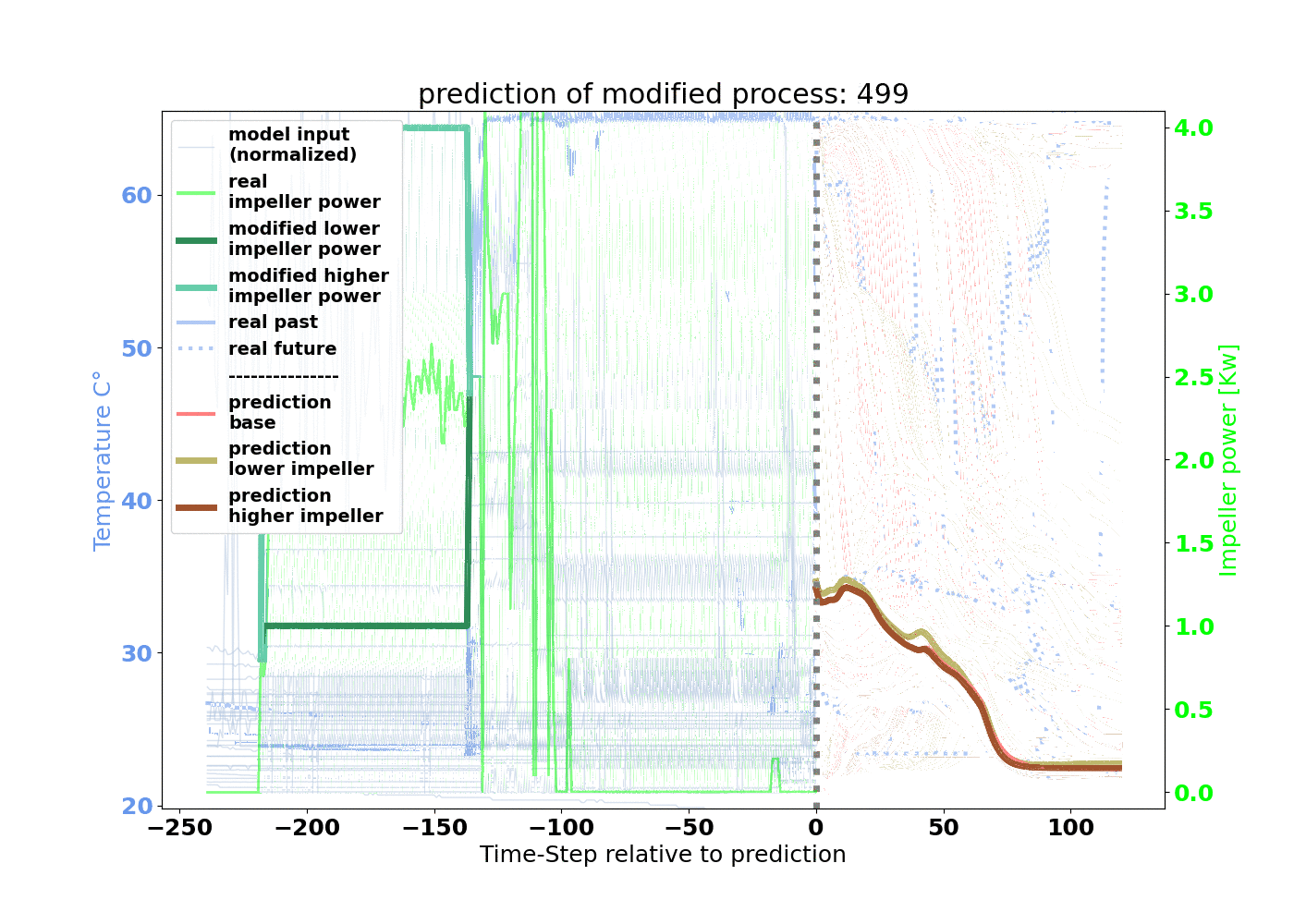
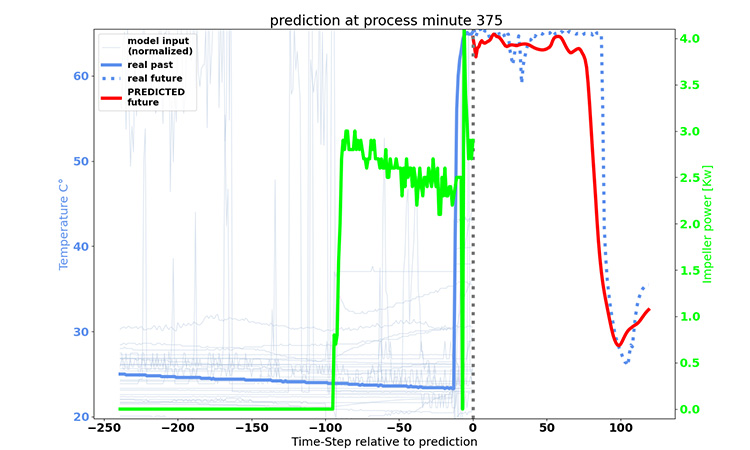
In our example, we wanted to shorten the drying duration to increase machine availability by finding an optimal LSTM configuration. The time-series data of the fluid bed dryer served as the input parameters for the model. For the output, or the target, we chose the parameter airflow temperature. The model response for this curve allows us to determine the drying duration.
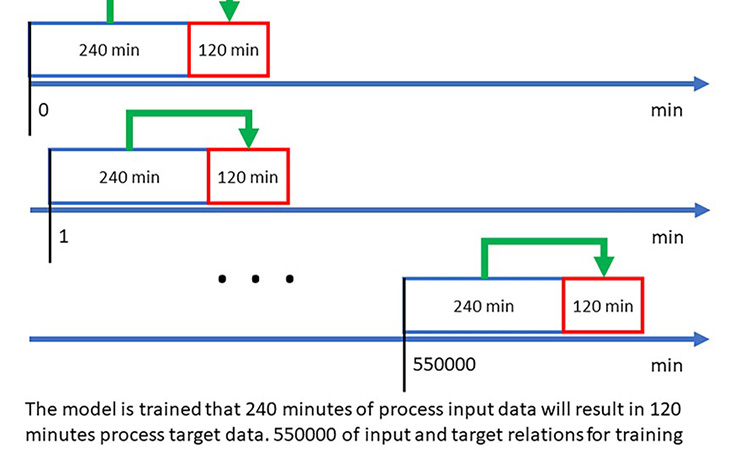
The model is trained that 240 minutes of process input data will result in 120 minutes of process target data. As depicted in Figure 3, 550,000 minutes of input and target relations for training are created by starting at minute 0 and increasing by 1 minute.